Самоучитель по 3dsmax 7
Сплайны Кочанека-Бартельса

![]() РАЗНОЕ
РАЗНОЕ
7.6. Сплайны Кочанека-Бартельса
Пусть у нас имеется набор моментов времени и заданные значения какой-то функции (например, координат положения объекта) в эти моменты. Для того, чтобы получить значение функции в какой-то промежуточный момент времени, между заданными моментами ее придется интерполировать. Самый простой случай, конечно, линейная интерполяция (точнее говоря, кусочно-линейная), когда между любыми двумя заданными точками p1, p2 значение интерполируется по следующей формуле:
f(t) = p1.value + (p2.value - p1.value) * t.
Здесь t - "локальное" время, t=0 в точке p1 и t=1 в точке p2, pi.value - значение интерполируемой величины в точке pi. Перевод "локального" времени t в "глобальное" время T и наоборот тривиален:
t = (T - p1.T) / (p2.T - p1.T),
T = p1.T + t * (p2.T - p1.T).
Результат получится такого вида:
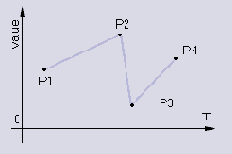
Но в результате такой интерполяции получаются ломаные - негладкие функции. Визуально это выливается во внезапно дергающиеся, неожиданно меняющие направление движения объекты и камеру. Негладкость можно математически описать как разрывность производной функции, получающейся в результате интерполяции; в точках задания значений у нас производная будет резко меняться.
Интерполяция сплайнами - такой метод, который дает в результате гладкую функцию.