Применяя алгоритм несколько раз, получаем методы отсечения в выпуклый полигон (например, прямоугольник...

Применяя алгоритм несколько раз, получаем методы отсечения в выпуклый полигон (например, прямоугольник, которым является экран) или выпуклый объем (например, ту часть пространства, которую видно из камеры).

Итак, пусть у нас есть полигон с N вершинами, заданными в каком-то порядке, то есть, по часовой стрелке или против; в каком именно, алгоритму все равно. Занумеруем их от 0 до N-1. Теперь последовательно обходим все ребра полигона: ребро от вершины 0 до вершины 1, от 1 до 2, ..., от N-2 до N-1, от N-1 до 0. Вершины, являющиеся началом и концом ребра, могут лежать в области отсечения, (область отсечения - либо полуплоскость для 2D случая, либо полупространство для 3D случая) могут и не лежать; возможны следующие случаи:

начало лежит в области отсечения, конец - тоже. Тогда просто добавляем начало к вершинам полигона-результата.
начало лежит в области отсечения, конец не лежит. В этом случае считаем точку пересечения ребра и границы области отсечения, добавляем в список вершин результата начало ребра и вслед за ним точку пересечения.
начало не лежит в области отсечения, конец лежит. Тоже считаем точку пересечения, и добавляем только ее.
начало не лежит в области отсечения, конец тоже. Переходим к следующему ребру, никак не изменяя результат.

Рассмотрим простенький пример работы алгоритма в 2D случае, а именно отсечем 2D треугольник прямой. Она делит плоскость на две полуплоскости, две области, нужную и ненужную.

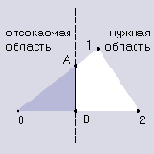
шаг 1, ребро 0-1: вершина 0 не лежит в нужной области, вершина 1 лежит.

Содержание раздела