Обработка звука в Adobe Audition 1.5
Анализируем запись и определяем стратегию обработки сигнала
Итак, запись звука с микрофона выполнена, и ее результаты сохранены в файле. Как вы уже знаете, работая над книгой, мы создали файл с примером EX03_01.WAV и поместили его в папку EXAMPLES на диск, сопровождающий книгу. Этот файл — часть проекта, целью которого является запись короткого видеоролика, содержащего звуковое сопровождение.
Выбор цели проекта не случаен. Мы считаем, что на практике это наиболее распространенная цель. Думаем, что многие читатели применяют или хотели бы применять компьютер для записи презентационного или рекламного видео/аудиоматериала.
Хочется, чтобы содержание ролика, который мы будем вместе создавать, было интересно и полезно нашим традиционным читателям — компьютерным музыкантам. Поэтому ролик посвящен аппаратуре, необходимой в продвинутой домашней звуковой студии. Съемки и звукозапись проводились на базе питерского магазина MusicLand. В качестве диктора и ведущего выступает его директор и давний участник проекта "Музыкальный компьютер" Вадим Лукин. Читателям он знаком по серии видеосюжетов, посвященных оборудованию домашней музыкальной студии. Эти видеосюжеты мы поместили на сопроводительный диск книги, посвященной программе Cakewalk SONAR [9].
По нашему замыслу ролик должен состоять из трех частей. В первой части Вадим Лукин приветствует зрителей-слушателей. Здесь звук записан одновременно с изображением, синхронизирован с ним и должен оставаться таковым после всех обработок. Во второй части ведущий за кадром перечисляет имеющееся звуковое оборудование. Его рассказ сопровождается видеорядом, составленным из цифровых фотографий. В третьей части ведущий в кадре приглашает нас в свою музыкальную страну. Здесь звук, как и в первой части, должен быть синхронизирован с изображением.
Методы записи и обработки синхронного и несинхронного звука различаются. В ближайших нескольких главах речь в основном будет идти об обработке звука, не зависящего от изображения.
До полного воплощения задуманного еще очень далеко. Сейчас нужно сделать очередной шаг: проанализировать полученную запись, оценить ее пригодность и наметить стратегию обработки, позволяющую устранить имеющиеся недостатки.
Давайте разберемся в том, какие средства анализа имеются в нашем распоряжении. Их не так много, но они достаточно эффективны:
мониторинг (прослушивание) записи; качественный визуальный и количественный (с помощью различных измерителей) анализ волновой формы и уровня записанного аудиосигнала; качественный визуальный и количественный анализ спектра (мгновенного и классического) записанного аудиосигнала.Рассмотрим каждое из направлений анализа подробнее.
Проводим мониторинг записи
Прежде всего записанный звук следует внимательно и многократно прослушать. Цель такого прослушивания состоит в том, чтобы оценить пригодность записи для дальнейшей обработки, а также отбраковать фрагменты, содержащие грубые ошибки. Если делалась многократная запись одного и того же материала, то на этом этапе следует выбрать дубли с самым высоким качеством записи. Если нет ни одного дубля, полностью от начала до конца пригодного для дальнейшей обработки, то можно выбрать несколько дублей. В дальнейшем следует смонтировать необходимую запись из лучших фрагментов, взятых из разных дублей. Если повторные записи выполнялись с перерывами, то дубли могут храниться в разных файлах. Мы создавали пример EX03_01.WAV, не прерывая запись, поэтому дубли идут один за другим. Правда, на самом деле, в первоначальном варианте файла EX03_01.WAV дублей было значительно больше, однако в целях экономии места на диске и вашего времени наиболее неудачные дубли (с оговорками диктора и слишком громкими посторонними звуками) мы вырезали.
Есть смысл прослушивать звук, одновременно просматривая соответствующую ему волновую форму (рис. 4.1).

Рис. 4.1. Так выглядит волновая форма, соответствующая файлу EX03_01.WAV
В файле EX03_01.WAV хранятся пять дублей записи одной и той же фразы. Итогом первого этапа анализа можно считать следующие выводы.
Первый дубль (фрагмент в интервале от 0:02 до 0:34) непригоден для дальнейшего использования из-за того, что в голосе человека, читавшего текст, иногда слышен хрип. В дальнейшем этот фрагмент волновой формы целесообразно вырезать, чтобы сократить размер файла и время его обработки. Второй дубль (от 0:37 до 1:13) записан с перегрузкой микрофона. Чело век, читающий текст, в ряде мест излишне акцентировал свою речь. По этому, хотя большинство максимумов волновой формы находится при мерно на уровне —6 дБ, встречаются отдельные выбросы, достигающие 0 дБ. Имеется также переполнение разрядной сетки АЦП, этот недостаток явился следствием того, что запись велась без компрессии. Дубль № 2 пока можно сохранить на тот случай, если в дальнейшем потребуется скомбинировать отдельные фрагменты, взятые из разных дублей. Третий дубль (от 1:16 до 1:49) содержит меньше материала с перегрузкой, чем дубль № 2, однако в нем нас не устроила интонация диктора, который к моменту записи этого дубля уже заметно устал, а его голос сник. Четвертый дубль (от 1:51 до 2:25), записанный после небольшой паузы, во время которой диктор отдохнул и осмыслил свою задачу, следует считать предпочтительным, хотя видно, что в нем тоже есть отдельные клиппированные отсчеты оцифрованного звука. Пятый дубль (от 2:27 до 3:01) записан без перегрузки. Устав "бороться" с диктором, который, увлекаясь, произносил некоторые слова значительно громче других, мы снизили уровень записи и отодвинули микрофон (петличный) дальше от его губ. Удаление микрофона от источника звука в свою очередь вызвало изменение звукового плана: на фоне несколько ослабленного прямого звука стал заметнее звук, отраженный стенами помещения и предметами, находящимися в нем. Иными словами, стала проявлять себя реверберация, в данном случае нежелательная, т. к. запись велась в не совсем подходящем для этой цели помещении, и такая реверберация, не украшая звук, снизила разборчивость речи. Тем не менее, и этот дубль в дальнейшем может быть выбран в качестве основного. Решение о том, какой дубль (№ 4 или № 5) следует использовать для сопровождения видеоряда в ролике, целесообразно принимать на последнем этапе. Ведь предстоит еще объединить в одном саундтреке три звуковых фрагмента: вступительную часть ролика, в которой звук синхронизирован с изображением диктора; несинхронное звуковое сопровождение видеоряда, составленного из изображений перечисляемых диктором элементов звуковой студии; заключительную часть ролика, в которой звук также синхронизирован с изображением диктора.Без анализа звука, соответствующего вступительной и заключительной частям ролика, заранее невозможно решить, какой из двух в принципе пригодных дублей подходит больше. Один из критериев совместимости фрагментов — степень сходства интонации диктора и звуковых планов фонограмм.
Прослушивая запись, следует одновременно наблюдать за измерителем уровня. С его помощью можно оценить уровень шума в паузе (в данном случае от —45 до —40 дБ), средний и максимальный уровень сигнала, обнаружить наличие перегрузки (см. разд. 3.3).
Получаем статистическую информацию о волновой форме с помощью окна Waveform Statistics
Сбор статистической информации о волновой форме осуществляется с помощью окна Waveform Statistics, открываемого командой Analyze > Statistics. Окно содержит две вкладки: General — статистическая информация о параметрах волновой формы и Histogram — гистограмма (распределение значений) отсчетов волновой формы.
Сведения, которые вы здесь получите, пригодятся и при решении вопроса о целесообразности борьбы с некоторыми искажениями, и при выборе параметров динамической обработки записанного сигнала.
Собираем информацию о волновой форме на вкладке General
Вкладка General (рис. 4.2) содержит статистическую информацию или о выделенном звуковом фрагменте, или обо всей волновой форме.

Рис. 4.2. Вкладка General окна Waveform Statistics
В столбцах для левого и правого стереоканалов (или в единственном столбце в случае монофонического сигнала) представлена следующая информация:
Minimum/Maximum Sample Value — минимальное/максимальное значение звукового отсчета; Peak Amplitude — пиковая амплитуда сигнала; Possibly Clipped Samples — количество отсчетов, имеющих уровень максимальной или минимальной границы характеристики аналого-цифрового преобразователя (клиппированных отсчетов); DC Offset — среднее значение отсчетов (уровень постоянной составляющей в выделенном фрагменте волновой формы); Minimum/Maximum RMS Power — минимальное/максимальное среднеквадратическое значение сигнала [12] (объем выборки задается в поле Window Width <...> ms, расположеннном в нижней части окна); Average RMS Power, Total RMS Power — варианты среднеквадратических значений сигнала; Actual Bit Depth — фактическая разрядность представления звуковых данных.Группа RMS Settings содержит опции, определяющие порядок измерения и вычисления среднеквадратического значения сигнала. OdB = FS Sine Wave — если выбран этот переключатель, среднеквадратическое значение сигнала измеряется таким образом, что синусоида максимальной допустимой амплитуды будет соответствовать 0 дБ RMS. OdB = FS Square Wave — если выбран этот переключатель, среднеквадратическое значение сигнала измеряется таким образом, что последовательность прямоугольных импульсов максимальной допустимой амплитуды будет соответствовать 0 дБ. Так как при равных амплитудах субъективная громкость последовательности прямоугольных импульсов на 3 дБ выше, чем громкость синусоидального колебания, при переключении опций OdB = FS Sine Wave и OdB = FS Square Wave происходит коррекция среднеквадратического значения сигнала на 3 дБ. Account for DC — если этот флажок установлен, то при вычислениях бу дет учтено наличие в аудиосигнале постоянной составляющей.
В поле Window Width <...> ms вы можете изменить размер временного окна, в котором программа измеряет RMS при поиске минимальных и максимальных значений.
Если вы решите изменить объемы выборок, то перерасчет среднеквадратического отклонения будет выполнен после нажатия кнопки Recalculate RMS.
Напротив большинства полей расположены кнопки с символом ->. При нажатии такой кнопки маркер в волновой форме устанавливается на отсчет, соответствующий тому или иному параметру.
Если вы хотите сохранить значения параметров в файле, чтобы в дальнейшем получить распечатку или вставить данные, например, в документ Microsoft Word, воспользуйтесь кнопкой Copy Data to Clipboard. Содержимое вкладки будет скопировано в буфер обмена.
Взгляните на статистические сведения файла ЕХ03_01.WAV.
| Mono | |
| Min Sample Value: | -32768 |
| Max Sample Value: | 32767 |
| Peak /Amplitude: | .03 dB |
| Possibly Clipped: | 190 |
| DC Offset: | -.395 % |
| Minimum RMS Power: | -60.23 dB |
| Maximum RMS Power: | -5.95 dB |
| Average RMS Power: | -24.3 dB |
| Total RMS Power: | -20.69 dB |
| Actual Bit Depth: | 16 Bits |
| Using RMS Window of 50 ms |
Обратите внимание на параметры:
Possibly Clipped = 190 — имеется 190 клиппированных отсчетов, они дают неприятный эффект "захлебывания", и их в дальнейшем предстоит обработать с целью восстановления формы сигнала на клиппированных участках; DC Offset = —.395 % — в волновой форме присутствует небольшая постоянная составляющая, что при монтаже может вызвать щелчки в местах склейки и разрезания фрагментов. От нее нам тоже нужно будет избавиться.Выделив поочередно каждый из пяти дублей, и проанализировав выделенные участки волновой формы, вы можете сравнить основные их параметры (табл. 4.1).
| Параметр | Дубль №1 | Дубль №2 | Дубль №3 | Дубль №4 | Дубль №5 |
|---|---|---|---|---|---|
| Possibly Clipped | 108 | 39 | 4 | 39 | 0 |
| Minimum RMS Power | -56.75 | -56.92 | -60.24 | -57.79 | -56.59 |
| Maximum RMS Power | -5.96 | -6.08 | -6.79 | -6.14 | -10.16 |
| Total RMS Power | -19.79 | -20 | -20.35 | -20.44 | -21.55 |
Сравнение соответствующих значений параметров убеждает в том, что по количеству клиппированных отсчетов (Possibly Clipped) выигрывают дубли № 3 и № 5. Дубль № 3, вероятно, наименее шумный (косвенно на это указывает наименьшее значение Minimum RMS Power). Самый "тихий" дубль № 3 (Total RMS Power), а самый "громкий" — дубль № 1, но он же и наиболее подвержен клиппированию (Possibly Clipped).
Значение параметра Total RMS Power для всех дублей мало (порядка -20 дБ). Речь будет звучать очень тихо по сравнению, например, с музыкой, наложенной с компакт-диска поверх речи. Поэтому на этапе сведения, возможно, потребуется компрессия динамического диапазона.
Анализируем распределение значений отсчетов на вкладке HistogramВкладка Histogram, содержащая гистограмму значений отсчетов выделенного фрагмента волновой формы, показана на рис. 4.3.
Гистограмма — широко распространенная (особенно в вероятностном анализе) форма представления информации о каком-либо случайном процессе. В данном случае гистограмма представляет собой график зависимости количества отсчетов, среднеквадратическое значение которых попадает в заданный интервал, от величины отсчета, выраженной в децибелах. Не очень понятно? Поясним на примере. На рис. 4.3 представлена гистограмма монофонической волновой формы, в которой содержится синусоидальный сигнал, сформированный с помощью команды Generate > Tones. В рассматриваемом случае заранее известно, что при формировании сигнала его амплитуда была установлена равной -3,2 дБ. Гистограмма совершенно верно отражает этот факт. Действительно, все 100% отсчетов попадают в интервал от -3,25 до —3,20 дБ. Отсчетов с большими значениями в анализируемом сигнале нет. Если вы захотите преобразовать амплитуду такого сигнала (усилить его), то можете смело установить любой коэффициент усиления, не превышающий 3,2 дБ. Искажения не появятся. Точно так же можно анализировать те сигналы, свойства которых неизвестны заранее. Результаты анализа пригодятся для принятия решения при любых преобразованиях амплитуды, например, при усилении сигнала или сжатии его динамического диапазона. Приведем еще один пример. На рис. 4.4 представлена волновая форма реального речевого сигнала, записанного в файле EX03_01.WAV (дубль № 4). Для вашего удобства мы выделили этот дубль в отдельный файл EX04_01.WAV.
Проанализируем гистограмму этого сигнала (рис. 4.5) и примем решение о том, как оптимально его обработать. Хорошо бы в будущем при минимальных искажениях максимально увеличить среднюю энергию сигнала (а тем самым — и субъективно ощущаемую громкость) и уменьшить уровень шума.
Во-первых, настораживает немонотонное поведение графика при уменьшении уровня сигнала (большие значения элементов гистограммы в области от —45 до —60 дБ). Похоже, эта волновая форма записана либо в неблагоприятных шумовых условиях, либо была использована аппаратура с высоким уровнем собственных шумов. На самом деле в данном случае запись велась на хорошей аппаратуре, но в помещении, где отсутствует звукоизоляция, а окна выходят на шумную улицу. Принимаем решение: отсчеты, значение которых меньше —45 дБ, — это шум. Поэтому одним из этапов динамической обработки может быть пороговое шумоподавление, причем исходное значение порога можно выбрать около —45 дБ. В процессе обработки его следует уточнить, контролируя результат на слух. Во-вторых, из анализа гистограммы следует, что доля отсчетов, уровень которых превышает —8 дБ, чрезвычайно мала, а превышающих —5 дБ — практически нет. Если точнее, то следует вспомнить, что Maximum RMS Power = -6.14 (см. Анализируем спектр сигналаКоманды View > Multitrack View, View > Waveform View и View > Spectral View переключают режимы отображения звуковой информации. Первому из перечисленных режимов посвящена гл. 10. Со вторым режимом вы уже знакомы, в нем мы работали до сих пор. В этих двух режимах звук представляется в виде волновых форм. Последняя команда включает режим отображения мгновенного спектра сигнала в виде градаций яркости и цвета. |
Знакомимся со спектральным анализом
О спектральной форме представления сигнала и, в частности, о мгновенном спектре детально рассказывается в книге [12]. Здесь же мы ограничимся лишь пояснениями, необходимыми для понимания сути спектрального анализа и основных терминов.
Начать знакомиться с сущностью спектральных представлений лучше с разложения в ряд Фурье периодического сигнала. Всякая периодическая функция (с ограничениями, носящими абстрактный характер) может быть представлена в виде разложения в ряд по тригонометрическим функциям — суммой слагаемых, каждое из которых есть не что иное, как косинусоидальное колебание с амплитудой 
![]() .
.
Совокупность коэффициентов 
![]() — его фазовым спектром.
— его фазовым спектром.
Частоты всех синусоидальных колебаний, из которых составляется периодическая функция s(t), кратны основной частоте F = 1/T. Отдельные составляющие называются гармониками. Колебание с частотой F называется первой гармоникой (к = 1), с частотой 2F— второй гармоникой (к = 2) и т. д.
Ряд Фурье дает разложение периодической функции по тригонометрическим функциям. Это разложение можно применить и к непериодической функции, которую рассматривают как предельный случай периодической функции при неограниченном возрастании периода. Если 
![]() , а
, а 
![]() — круговая текущая частота, изменяющаяся непрерывно) и ряд Фурье превращается в интеграл Фурье. Непериодическая функция может быть представлена только суммой бесконечно большого числа бесконечно близких по частоте колебаний с бесконечно малыми амплитудами. Интеграл Фурье представляет непериодическую функцию суммой синусоид и косинусоид с непрерывной последовательностью частот. Иногда говорят, что в составе непериодического сигнала есть колебания всех частот. В случае непериодического сигнала говорить об амплитудах отдельных спектральных составляющих нет смысла, т. к. это бесконечно малые величины.
— круговая текущая частота, изменяющаяся непрерывно) и ряд Фурье превращается в интеграл Фурье. Непериодическая функция может быть представлена только суммой бесконечно большого числа бесконечно близких по частоте колебаний с бесконечно малыми амплитудами. Интеграл Фурье представляет непериодическую функцию суммой синусоид и косинусоид с непрерывной последовательностью частот. Иногда говорят, что в составе непериодического сигнала есть колебания всех частот. В случае непериодического сигнала говорить об амплитудах отдельных спектральных составляющих нет смысла, т. к. это бесконечно малые величины.
Классическое определение спектра основывается на преобразовании Фурье, причем интегрирование по времени выполняется в бесконечных пределах и спектр зависит только от частоты. Однако бесконечная длительность какого-либо процесса — это абстракция, не имеющая ничего общего с реальностью.
Если анализируемая функция есть отображение некоторого реального физического процесса, то сведения о спектре мы получаем лишь в результате наших наблюдений. Следовательно, при анализе спектра мы можем выполнить вычисления лишь от момента начала наблюдения до текущего момента времени t, а не до момента, устремленного в бесконечное будущее.
Текущий спектр определяется как результат преобразования Фурье, но с переменным верхним пределом интегрирования, в качестве которого фигурирует текущее время. Поэтому текущий спектр является функцией не только частоты, но и времени.
В начале раздела мы воспользовались понятием периодической функции. На самом деле периодическая функция — лишь весьма полезная математическая абстракция. Ведь всякий природный процесс имеет начало и конец.
Принято называть реальный циклический процесс периодическим, если он длится достаточно долго. Мерилом длительности служит число "периодов", которое должно быть намного больше единицы. Периодичность процесса проявляется лишь с течением времени, когда прорисовываются его характерные черты. Текущий спектр и отражает это развитие процесса. Таким образом, периодический процесс — это предел, к которому может стремиться с течением времени реальный повторяющийся процесс. Аналогично и спектр (в его классическом определении) такого процесса есть предел, к которому стремится текущий спектр при увеличении времени интегрирования до бесконечности. Например, при интегрировании в бесконечных пределах спектр синусоиды представляет собой единственную линию на частоте, равной частоте этой синусоиды.
Но как на практике измеряется текущий спектр, например, той же синусоиды? Мы включаем анализатор спектра, а спустя какое-то время выключаем его. Получается, что измеряется не спектр бесконечного синусоидального колебания, а спектр его более или менее протяженного отрезка. Это значит, что фактически исследуется спектр прямоугольного импульса с синусоидальным заполнением. Сказанное объясняет причину того, что даже для синусоидального колебания при уменьшении времени интегрирования спектральная линия расширяется, появляются боковые лепестки спектральной функции, ее нули все больше удаляются друг от друга. Ведь именно так и должен вести себя спектр прямоугольного импульса при уменьшении его длительности [12].
Таким образом, текущий спектр в большей степени отражает свойства сигналов, проявляющиеся в реальных условиях их генерирования и обработки, нежели спектр, полученный на бесконечном временном интервале.
Текущий спектр — только мостик от частотного к временному описанию процесса. Не только спектр, вычисленный на бесконечном временном интервале, но и текущий спектр — слишком грубый инструмент в тех случаях, когда анализируемый процесс не стационарен. Для того чтобы сблизить частотное и временное представления сигнала, было введено понятие мгновенного спектра. Мгновенный спектр — это спектр короткого отрезка процесса, непосредственно предшествующего данному моменту времени. В этом определении мы имеем дело со скользящим интегрированием: интервал интегрирования имеет постоянную длину, но перемещается по оси времени. А вот относительно текущего времени этот интервал расположен неизменно. Страшно далеко это определение спектра от того, что давно придумали великие математики! И все же в руках звукорежиссера именно мгновенный спектр является наиболее эффективным инструментом анализа свойств записываемого или уже записанного звука. Музыка, которую создают с помощью синтезатора, отличается особенно заметной нестационарностью тембра. Может быть, именно поэтому в звуковых редакторах уже давно используются средства анализа текущего и мгновенного спектра.
Вы познакомились с тремя подходами к вычислению спектра. Но это еще не финал. Продолжим погружение в спектральные преобразования. И вновь речь пойдет о влиянии времени на результаты спектрального анализа.
Как вычисляется одна-единственная точка графика спектра? Исчерпывающий ответ на этот вопрос дают формулы. Но прибегать к ним не хочется, лучше попытаемся разъяснить суть дела обычными словами.
Итак, сначала выбирается частота 
 , с шагом
, с шагом 
 , тем лучше) в моменты времени
, тем лучше) в моменты времени 
В некоторый момент процесс измерения спектра на частоте 
 (выбирается новое значение частоты
(выбирается новое значение частоты 
 не будет перекрыт весь заданный диапазон.
не будет перекрыт весь заданный диапазон.
Описанная выше процедура вычисления спектрального коэффициента есть не что иное, как вычисление взаимокорреляционной функции исследуемого сигнала и синусоиды заданной частоты. Иными словами, в процессе вычисления спектральной составляющей выясняется степень сходства исследуемого сигнала со стандартным (базисным) сигналом, в данном случае — с синусоидой. Можно сказать и так: выясняется, в какой пропорции синусоида "содержится" в исследуемом сигнале.
Если исследуемый сигнал уже записан, и в нашем распоряжении есть цифровой анализатор спектра, способный сколь угодно долго хранить результаты промежуточных вычислений, то измерение текущего спектра и мгновенного спектра вполне осуществимо по описанной выше процедуре.
Уместен вопрос: вполне ли адекватен описанный математический алгоритм тому спектральному анализу, который проводят реальные анализаторы спектра, и тому, который выполняют органы слуха и мозг человека? Ответ: нет, не вполне.
Основная проблема состоит в том, что прибор, анализирующий спектр, и человек обладают конечной памятью. Былые события, подробности хода любого процесса постепенно стираются в ней. Это означает, что чем больше удалены в прошлое отсчеты анализируемого сигнала, тем меньший вклад они вносят в накопление той самой суммы произведений отсчетов, которая, в конце концов, определяет значение спектрального коэффициента.
Учет реальных свойств памяти анализаторов спектра осуществляется с помощью весовых функций. Весовая функция описывает зависимость вклада предшествующих отсчетов исследуемого сигнала в вычисляемый спектр. Наглядное представление о весовой функции дает форма так называемого спектрального окна.
Тот спектральный анализ, о котором мы вели речь до сих пор, соответствует спектральному окну прямоугольной формы: весовая функция равна единице в пределах спектрального окна и равна нулю вне его. При анализе текущего спектра начало спектрального окна совпадает с началом отсчета времени, а конец приходится на текущий момент времени. Текущее время идет вперед, правая граница спектрального окна смещается, поэтому каждому конкретному моменту времени завершения анализа соответствует своя ширина спектрального окна. Если вычисляется мгновенный спектр, то спектральное окно скользит вдоль оси времени, не изменяя своей ширины.
Однако в большей степени суть реального спектрального анализа отражает экспоненциальная весовая функция.
Прямоугольное и экспоненциальное спектральные окна используются при вычислении спектра наиболее часто. Первое соответствует идеальному анализатору с бесконечно большой памятью, второе удачно отражает свойства человеческого мозга и реальных анализаторов спектра на основе резонансных фильтров. Наряду с этими, хотя не столь широко, применяются и другие весовые функции. Трудно дать конкретные рекомендации по поводу предпочтительности использования той или иной из них. Пожалуй, единственный совет может состоять в том, что следует остановиться на какой-то одной весовой функции. Только тогда у вас будет уверенность в том, что различия результатов анализа обусловлены различием свойств сигналов, а не методов расчета. Целесообразно также выбирать одну и ту же весовую функцию, когда при работе с одним и тем же сигналом вы решаете несколько задач, в которых применяются спектральные преобразования.
До сих пор, знакомясь с сущностью спектральных представлений, мы предполагали, что сигнал является аналоговым, т. е. описывается непрерывной функцией. На самом деле компьютер способен обрабатывать только цифровые сигналы — дискретные во времени и квантованные по уровню. Поэтому аналоговый сигнал подвергается аналого-цифровому преобразованию (АЦП). Затем с сигналом в цифровой форме выполняются все необходимые операции, в частности, спектральный анализ, причем вместо обычного спектрального преобразования производится так называемое дискретное преобразование Фурье (ДПФ). Непрерывное время и непрерывная частота заменяются на соответствующие дискретные величины, а вместо интегрирования выполняется суммирование.
Чтобы провести дискретное преобразование Фурье для последовательности из N элементов, требуется выполнить N2 операций с комплексными числами. Если длины обрабатываемых массивов цифровых отсчетов звуковых колебаний имеют порядок тысячи и больше, то использовать эти алгоритмы дискретного спектрального анализа затруднительно (особенно в реальном времени). Выходом из положения явился алгоритм быстрого преобразования Фурье (БПФ). Значительно сократить число выполняемых операций здесь удается за счет того, что обработка входного массива сводится к нахождению ДПФ массивов с меньшим числом элементов.
Приближенно можно считать, что объем вычислений по алгоритму БПФ пропорционален произведению N x log2N, где N — количество отсчетов сигнала. А если решать задачу расчета спектра "в лоб", не пользуясь алгоритмами быстрых преобразований, то объем вычислений ориентировочно будет пропорционален произведению N x N. Если бы не БПФ, то для фильтрации, спектрального анализа и синтеза сигналов не хватило бы быстродействия самого современного компьютера.
Анализируем мгновенный спектр сигнала в режиме Spectral View
Команда View > Spectral View включает режим отображения мгновенного спектра сигнала в виде градаций яркости и цвета. На рис. 4.6 показано распределение мгновенного спектра сигнала, записанного в файле EX03_01.WAV.

Рис. 4.6. Представление звукового сигнала в виде мгновенного спектра
О чем говорит картинка, которую мы видим в режиме Spectral View? Как можно использовать информацию, полученную путем наблюдения мгновенного спектра?
По горизонтальной оси отложено время, по вертикальной — частота. Цвет и яркость отображения зависят от уровня спектральной составляющей в анализируемой волновой форме на той или иной частоте (чем ярче — тем выше уровень). Что касается цвета, то, например, по умолчанию нулевой уровень соответствует черному цвету, по мере увеличения уровня появляется красный цвет, а максимальный уровень отображается белым цветом. Цветовую гамму можно сменить, воспользовавшись опциями страницы Spectral вкладки Colors диалогового окна Settings.
Рассматривая спектральную диаграмму, можно составить представление о частотной области сосредоточения основной доли энергии сигнала в различных точках волновой формы. Эта информация полезна при сведении нескольких треков в микс. Желательно, чтобы спектры сигналов треков существенно не перекрывались по частоте. Добиться этого можно путем фильтрации. В процессе обработки сигналов фильтрами можно увидеть и сравнить с помощью спектральных диаграмм спектр сигнала, полученного в результате обработки, со спектром исходного сигнала и тем самым оценить, верно ли ведется обработка.
Чрезвычайно важно то обстоятельство, что Adobe Audition в режиме Spectral View позволяет не только наблюдать за спектром сигнала, но и редактировать волновую форму. Не понравившийся вам чем-либо фрагмент можно выделить и основательно с ним поработать (вплоть до вырезания).
В качестве примера на рис. 4.7 показан мгновенный спектр небольшого участка волновой формы из файла EX03_01.WAV. Для того чтобы лучше разглядеть детали, мы выделили этот фрагмент и скопировали его в файл EX04_02.WAV.

Рис. 4.7. Пример мгновенного спектра, содержащего аномалию
Это мгновенный спектр сигнала, представляющего собой дикторский текст. Области с относительно широким спектром соответствуют словам, с узким — паузам между ними. Видно, что в конце первой фразы (где расположен указатель мыши) мгновенный спектр шире, чем в ближайших окрестностях. В этом месте наблюдается некий неестественный, подозрительный выброс. Широкий спектр всегда соответствует быстрому перепаду значений сигнала или короткому импульсу. Скорее всего, в этом месте есть щелчок. В принципе можно было бы выделить участок, посредине которого находится этот пик, подравнять область выделения по нулевым уровням сигнала и нажать клавишу <Delete>. Щелчок был бы удален. Когда вы наберетесь опыта, в подобных случаях можно так и поступать. А пока нелишним будет посмотреть на предполагаемый пик. Для этого в меню View выберем команду Waveform View. В главном окне появится знакомое изображение звуковой волны (рис. 4.8). Отображается тот же фрагмент волновой формы, спектр которого мы видели на рис. 4.7, интервал с аномалией выделен.

Рис. 4.8. Загадочный пик обнаружен
А вот и "герой нашей повести" — маленький, едва заметный остренький пичок, соответствующий отметке 1.0 на шкале времени. Он так мал, что даже когда знаешь, что и где искать, найти его очень трудно. А представьте себе, что мы пытались бы обнаружить этот выброс, просматривая звуковую волну! Скорее всего, даже если искать очень тщательно и неспешно, он бы так и остался незамеченным.
Может быть, ничего страшного и не произошло бы, пропусти мы эту аномалию? Чтобы ответить на этот вопрос, достаточно прослушать участок волновой формы, включающий обнаруженный объект. Звучит он очень заметно и неприятно: "плямк" — звук при резком размыкании губ, склеившихся в паузе между словами.
Изучая спектральное представление, можно обнаружить любые ненормально быстрые перепады значений сигнала. Часть из них может быть вызвана внешними причинами: щелчки, трески, дефекты речи и т. п. Иногда скачки значений отсчетов появляются в самой программе в результате неграмотного монтажа фонограммы. Например, монтируются фрагменты разных сигналов, и хотя бы один из них имеет постоянное смещение или сверхнизкочастотную составляющую. Или при нарезке фрагментов звукооператор не позаботился о том, чтобы точки разрезов совпадали с нулевыми точками звуковой волны.
Проводим спектральный анализ с помощью окна Frequency Analysis
Было бы странно, если бы такой редактор, как Adobe Audition, не предоставлял возможность проведения классического спектрального анализа. И действительно, такое средство имеется, а доступ к нему осуществляется из меню Analyze.
Командой Analyze > Show Frequency Analysis откройте окно спектрального анализатора Frequency Analysis (рис. 4.9).

Рис. 4.9. Окно спектрального анализатора
Когда вы открываете окно Frequency Analysis, происходит предварительный расчет спектра короткого фрагмента волновой формы, начало которого совпадает с позицией маркера. Если же выделен фрагмент волновой формы (или даже вся волновая форма), анализируется выборка сигнала, расположенная посередине выделенного фрагмента. Это соответствует измерению единственного значения мгновенного спектра.
Если анализировать спектр в процессе воспроизведения волновой формы, то картинка как бы оживет: в окне Frequency Analysis будет отображаться последовательность значений мгновенного спектра. Аналогичный результат можно получить и не включая режим воспроизведения. При открытом окне Frequency Analysis в главном окне программы следует захватить мышью и буксировать влево или вправо один из желтых треугольников, расположенных над и под рабочим полем и жестко связанных с маркером (вертикальной желтой пунктирной линией).
Чтобы выполнить спектральный анализ всего выделенного звукового фрагмента (или всей волновой формы), нажмите кнопку Scan. Спустя некоторое время после завершения расчета спектра изображение изменится. Полученный результат приближенно соответствует классическому спектру: измерение производится на большом, хотя, разумеется, не бесконечном интервале.
Расчет спектра производится раздельно для правого и левого каналов. На графике кривые спектрограмм для разных каналов отображаются разными цветами.
Если окно с графиком спектра покажется мелковатым, вы можете увеличить его традиционным способом — с помощью мыши.
А теперь рассмотрим график внимательнее. По горизонтальной оси откладывается частота в герцах, по вертикальной — уровень компонентов сигнала на этой частоте.
При установленном флажке Linear View горизонтальная ось размечается в линейном масштабе. В линейном масштабе удобнее рассматривать весь спектр в целом, включая его высокочастотную область. Если этот флажок снят, то по горизонтали устанавливается логарифмический масштаб. Напомним, что логарифмический масштаб позволяет наблюдать низкочастотную часть спектра в деталях. Для сравнения на рис. 4.10 при логарифмической шкале по оси частот показан спектр того же сигнала, для которого на рис. 4.9 выбран линейный масштаб.

Рис. 4.10. Спектр сигнала при логарифмическом масштабировании оси частот
Слева под шкалой частот располагается поле, в котором отображаются данные о значениях спектральной функции сигналов правого и левого канала для той частоты, на которую в данный момент нацелен указатель мыши (сама частота также отображается в этом поле). Сказанное справедливо при условии, что указатель мыши находится в пределах координатного поля. При перемещении указателя мыши значения параметров изменяются. Если указатель мыши находится вне пределов координатного поля, то значения трех отображаемых параметров не меняются, причем они соответствуют той частоте, при которой указатель мыши, покидая координатное поле, пересек его границу.
Обратите внимание на то, что числа, отображаемые в поле Cursor, строго говоря, не являются координатами указателя мыши. В этом поле вы видите координату указателя мыши на оси частот и соответствующее ей значение спектра. Это упрощает процесс численного измерения значений спектра. Вам не нужно прицеливаться в конкретную точку на координатной плоскости. Достаточно добиться, чтобы в поле Cursor появилось искомое значение частоты, а значение спектра для нее программа предъявит вам автоматически.
В поле, расположенном правее рассмотренного, показаны частоты спектральных составляющих сигналов левого и правого каналов, в окрестностях которых сосредоточена максимальная энергия (частоты максимальных пиков на графике). Здесь же указывается условное обозначение высоты тона, соответствующего частоте максимума спектральной функции (отдельно для правого и левого каналов).
Используются стандартные обозначения нот: С, D, E, F, G, А, В. На рис. 4.10 для левого канала это G. Числа в скобках обозначают:
номер октавы (0 — субконтроктава, 1 — контроктава, 2 — большая окта ва, 3 — малая октава и т. д.); на рис. 4.10 — это 2; расстройку относительно точного значения высоты предполагаемого тона в центах (цент — сотая доля полутона) с указанием знака расстройки; на рис. 4.10 — это -1.На рис. 4.10 измеренная частота максимума спектральной функции составляет 97,891 Гц — несколько меньше частоты ноты G2, которая в соответствии со стандартом "А4 = 440 Гц" равна 97,998 Гц. Следовательно, высота тона (G2 -1), которая оказалась на 1 цент ниже тона G2, распознана программой верно.
Примечание
Частоты максимумов спектральной функции для сигналов правого и левого каналов могут быть различными. В верхней части окна отображается высота тона, соответствующая сигналу в левом канале.
В правом верхнем углу окна расположена группа Hold, включающая в себя 4 цветные кнопки. Если не нажата ни одна из кнопок, то огибающие спектральных функций сигналов правого и левого каналов отображаются линиями разного цвета. Если нажата хотя бы одна кнопка, то огибающие спектральных функций сигналов правого и левого каналов отображаются разными оттенками одного и того же цвета. Предусмотрено 4 цвета: зеленый, красный, синий и желтый. Если нажать несколько кнопок, то высшим приоритетом будет обладать та из них, которая находится правее.
В левом нижнем углу окна расположен раскрывающийся список, предназначенный для выбора одного из 5 стилей отображения спектральной функции.
Lines — отображается только огибающая спектральной функции. Area (Left on top) — отображаются и огибающая спектральной функции, и ее заполнение: часть координатной плоскости, находящаяся под огибающей, залита цветом, спектр сигала левого канала отображается в верхнем слое рисунка, правого — в нижнем. Area (Right on top) — отображаются и огибающая спектральной функции, и ее заполнение; спектр сигала правого канала отображается в верхнем слое рисунка, левого — в нижнем. Bars (Left on top) — заполнение спектральной функции отображается в виде вертикальных полосок. Спектр сигала левого канала отображается в верхнем слое рисунка, правого — в нижнем. Bars (Right on top) — заполнение спектральной функции отображается в виде вертикальных полосок. Спектр сигала правого канала отображается в верхнем слое рисунка, левого — в нижнем.Если анализируется монофонический сигнал, то выбирать можно только из трех вариантов отображения — ведь в этом случае нет слоев изображения.
Нажав кнопку Advanced, вы увеличите число доступных опций окна. Дополнительно появятся:
поле Reference <...> dBFS; раскрывающийся список FFT Size; раскрывающийся список, предназначенный для выбора типа весовой функции; кнопка Copy to Clipboard, позволяющая переслать значения частот и соответствующие им значения спектральной функции в текстовом формате в буфер обмена.Возможно, вам понадобится сместить график по вертикали, чтобы рассмотреть в подробностях поведение спектральной функции на каком-либо ее конкретном участке. В поле Reference <...> dBFS вы можете задать величину смещения графика спектра по вертикали относительно нулевого уровня. Не забудьте установить нулевое значение этого параметра перед тем, как приступить к численному измерению абсолютных значений спектральной функции для тех или иных частот. В противном случае в измерениях будет присутствовать систематическая погрешность, по абсолютной величине равная введенному вами смещению.
В раскрывающемся списке FFT Size предусмотрено несколько стандартных значений размера выборки для БПФ (чем больше это значение, тем точнее анализ, и тем больше время, необходимое для его проведения), а в раскрывающемся списке, расположенном правее, — различные вариации этого преобразования, каждая из которых имеет свои достоинства и недостатки.
Окно спектрального анализатора не является модальным, т. е. оно существует как бы независимо от главного окна программы. Иными словами, окно Frequency Analysis может находиться в открытом состоянии и в то время, когда вы работаете в главном окне (выделяете фрагмент волновой формы, перемещаете маркер, генерируете звуковые колебания и т. д.). Все изменения, происходящие с волновой формой, немедленно отражаются и на спектре. Это сделано специально для удобства пользователя: вы можете работать с волновой формой и тут же видеть результат спектрального анализа. Кроме того, если размер выборки при БПФ задан относительно небольшим, например, 4096 или менее (для процессора с тактовой частотой 800 МГц), можно воспроизводить звук и одновременно наблюдать за динамикой изменения его спектра.
Следует отметить, что окно Frequency Analysis является плавающим. При желании его можно пристыковать к границе главного окна.
Обращаем ваше внимание на то, что предел изменения частоты по горизонтальной оси в окне Frequency Analysis устанавливается автоматически. Он зависит от частоты дискретизации анализируемой волновой формы.
Присмотревшись, можно заметить, что при переходе от линейного к логарифмическому масштабу максимальная отображаемая частота изменяется.
Обладая некоторым опытом общения с анализатором и профессиональным чутьем, по спектру сигнала вы сможете, например, разыскать на графике даже небольшой выброс, в котором сосредоточена основная энергия помехи, а затем с помощью фильтра удалить этот выброс из спектра сигнала, существенно улучшив при этом отношение полезного сигнала к шуму.
Проведем анализ спектра звукового сигнала из файла EX04_01.WAV. Результат представлен на рис. 4.11.

Рис. 4.11a. Спектр сигнала, записанного в файле EX04_01.WAV: линейный масштаб.
Напомним, что по результатам анализа гистограммы мы сделали вывод о том, что компоненты фонограммы с уровнем меньше примерно -45 дБ представляют собой шум. На рис. 4.11, а видно, что спектральная функция уменьшается до такого уровня примерно на частоте 14 кГц. Все спектральные компоненты, лежащие выше этой границы, обусловлены шумом и в дальнейшем их можно смело подавить фильтром. В принципе, если даже в данном случае срезать верхние частоты не с 14 кГц, а с 11 кГц, то ущерб качеству звучания сигнала нанесен не будет. Опыт подсказывает, что небольшое (в пределах от 4 дБ до 6 дБ) увеличение значений спектральной функции в области частот 11 кГц—14 кГц, вероятнее всего, обусловлено высокочастотным широкополосным шумом, избавиться от которого было бы полезно.
Теперь обратите внимание на рис. 4.11, б. На нем хорошо видна низкочастотная часть спектра. Здесь в глаза бросается большой уровень низкочастотных (меньше 80 Гц) и сверхнизкочастотных (меньше 20 Гц) составляющих, не характерных для речи. Это тоже шум — его издают автомобили, проезжающие под окнами здания по оживленному Московскому проспекту. Словом, в дальнейшем можно будет подавить с помощью фильтра и составляющие спектра сигнала, лежащие ниже 80 Гц

Рис. 4.11b. Спектр сигнала, записанного в файле EX04_01.WAV: логарифмический масштаб.
Контролируем моносовместимость сигнала с помощью окна Phase Analysis
Вообще-то сигнал из файла EX03_01.WAV является монофоническим и применительно к нему проблема контроля моносовместимости неактуальна. Он, безусловно, моносовместим. Такого рода контроль вам понадобится выполнять позже, когда в вашем распоряжении появятся стереофонические треки. Однако мы решили познакомить вас с возможностями окна Phase Analysis именно сейчас, в главе, посвященной всем имеющимся в программе средствам анализа оцифрованного звука.
Если вы планируете воспроизводить звуковой материал в монофоническом режиме (например, по телевидению), то должны быть уверены в его моносовместимости.
Моносовместимость важна и при передаче музыкальных композиций по радио, даже если передача ведется радиостанцией, осуществляющей стереофоническое вещание. Все дело в том, что определенная часть аудитории любой радиостанции принимает ее программы с помощью монофонических приемников. Разработчики существующих стандартов формирования стереосигналов исходили из необходимости выполнения требования совместимости стереофонической передачи с монофоническим оборудованием. Не случайно в эфир передаются не сигналы левого и правого каналов (L и R), а их сумма (L + R) и разность (L — R).
В низкочастотный тракт монофонического приемника попадает лишь суммарный сигнал, и вы можете, хоть и в монофоническом формате, но все же без каких-либо других потерь слышать все звучащие инструменты и голоса, в какой бы точке исходной стереопанорамы они ни находились.
В декодер стереофонического радиоприемника попадают и суммарный, и разностный сигналы. Там эта парочка разводится по двум каналам обработки. В одном канале сигналы, поступившие из эфира, складываются, а в другом — вычитаются. Не нужно быть профессиональным математиком для того, чтобы убедиться в справедливости элементарных преобразований:
(L + R) + (L — R) = 2L — выделен и усилен в 2 раза сигнал левого канала (L); (L + R) - (L - R) = 2R — выделен и усилен в 2 раза сигнал правого канала (R).Несовместимость музыкальной композиции с монофоническим оборудованием появляется тогда, когда компоненты звукового сигнала левого и правого каналов оказываются в противофазе. Вы уже знаете, что при преобразовании стереосигнала в монофонический сигналы левого и правого каналов суммируются. При этом звуковые компоненты, находящиеся в противофазе, "гасят" друг друга, в результате чего возникают неприятные на слух искажения. Партии некоторых инструментов могут вообще "исчезнуть" из композиции. В первую очередь это утверждение относится к партиям, панорамированным в центр.
В компьютерной музыке такая ситуация не может возникнуть сама по себе. Как правило, она является следствием применения специальных эффектов, изменяющих фазу звукового сигнала.
Определить на слух моносовместимость фонограммы способен далеко не каждый звукорежиссер. Для этой цели есть специальные устройства — контрольные дисплеи стереозвука, или стереогониометры, позволяющие анализировать множество параметров звукового сигнала, в том числе фазовые соотношения между одноименными спектральными компонентами в разных каналах.
В Adobe Audition есть возможность контроля моносовместимости сигнала с помощью встроенного в программу виртуального стереогониометра — окна Phase Analysis (рис. 4.12), открываемого командой Analize > Show Phase Analysis.

Рис. 4.12. Окно Phase Analysis; выбрана система координат M/S
Виртуальный фазовый анализатор, о котором сейчас пойдет речь, обладает функциональными возможностями, реализованными далеко не во всех его "железных" собратьях (разве что в самых дорогих). Судите сами. С помощью окна Phase Analysis можно:
проводить анализ в реальном времени; получать усредненную картину для всей волновой формы; наблюдать мгновенную диаграмму, соответствующую текущему положению маркера; исследовать выделенные фрагменты волновой формы, имеющие произвольную протяженность во времени; отображать результаты измерений в двух различных системах координат.Кроме координатного поля, в окне Phase Analysis еще есть только три элемента.
Normalize — кнопка, нажав которую, вы нормализуете результаты измерения параметров сигнала таким образом, что изображение займет максимальную допустимую область координатного поля. Mid/Side — кнопка, предназначенная для переключения системы координат, где графически отображаются результаты измерений. Выбрать можно из трех вариантов: Mid/Side ("середина/стороны" или "моно/ стерео", см. рис. 4.12), Left/Right ("левый/правый", рис. 4.13) и Spin ("ле вый/правый с вращением развертки изображения", рис. 4.14). Samples — раскрывающийся список, позволяющий задать количество от счетов в анализируемом сигнале, на основе которых программа выполнит быстрое преобразование Фурье и вычислит фазовые сдвиги. Чем больше число, выбранное в этом списке, тем выше точность вычислений, но и тем больше времени они займут.
Рис. 4.13. Окно Phase Analysis. Выбрана система координат L/R

Рис. 4.14. Окно Phase Analysis. Выбран вариант отображения Spin
Окно Phase Analysis, как и рассмотренное в предыдущем разделе окно анализатора спектра, — немодальное, поэтому когда оно открыто, можно работать с элементами управления, расположенными в главном окне. В частности, можно воспроизводить записанные волновые формы и наблюдать игру красок и форм оживших графиков фазового анализатора. Кроме того, окно Phase Analysis плавающее, его можно пристыковать к границе главного окна.
Итак, с технической точки зрения применение окна Phase Analysis не составляет труда: открыли — и смотрите. Вопрос в том, что можно здесь увидеть. Прежде чем ответить на него, нужно разобраться в том, что такое фигуры Лиссажу, как они получаются и какую информацию в себе несут.
Фигурами Лиссажу называются траектории точки, одновременно совершающей гармонические колебания в двух взаимно перпендикулярных направлениях. Траектория точки — замкнутая кривая, форма которой зависит от соотношений амплитуд, частот и начальных фаз колебаний.
Текущие координаты x(t) и y(t) точки определяются системой выражений:

где 
![]() — начальные фазы колебаний.
— начальные фазы колебаний.
Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат (ОХ и О У) и расположены по обеим сторонам от них на расстояниях, соответственно равных А2 и А1.
Отношение частот 
![]() складываемых колебаний равно отношению числа касаний (узловых точек) соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной оси ОУ, к числу ее касаний со стороной прямоугольника, параллельной оси ОХ.
складываемых колебаний равно отношению числа касаний (узловых точек) соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной оси ОУ, к числу ее касаний со стороной прямоугольника, параллельной оси ОХ.
Во времена, когда об электронно-счетных частотомерах никто даже не мечтал, да и позже, когда они все еще оставались большой редкостью, с помощью фигур Лиссажу измеряли неизвестную частоту колебания, сравнивая ее с частой колебания эталонного.
Измерительным прибором может служить осциллограф. На пластины, отклоняющие светящуюся точку экрана в вертикальном направлении, как обычно, подают исследуемое колебание. Но, в отличие от традиционного режима работы прибора, на горизонтально-отклоняющие пластины электронно-лучевой трубки не подают сигнал, создающий временную развертку наблюдаемого процесса. Вместо него подключают эталонное гармоническое колебание. Наблюдая фигуры Лиссажу, сравнивая их с образцовыми изображениями и подсчитывая узловые точки, определяют разность фаз, отношение амплитуд и отношение частот колебаний.
Описанный принцип действия лежит в основе стереогониометра. Виртуальный аналог прибора встроен в Adobe Audition, а доступ к нему осуществляется посредством окна Phase Analysis. Работа стереогониометра поясняется схемой, представленной на рис. 4.15.

Рис. 4.15. Схема, поясняющая принцип действия стерестониометра
На два входа прибора подаются сигналы левого (L) и правого (R) каналов. Суммарно-разностным преобразователем, выполняющим функцию, обратную функции стереодекодера радиоприемника, эти сигналы преобразуются в:
суммарный сигнал М = L + R (монофоническая компонента); разностный сигнал S = L — R (стереофоническая компонента).Усиленные сигналы подаются на пластины электронно-лучевой трубки: М — на вертикально-отклоняющие, a S — на горизонтально-отклоняющие. Так складываются колебательные движения светящейся точки экрана в двух взаимно перпендикулярных направлениях — в системе координат M/S (Моно/ Стерео), т. е. образуются фигуры Лиссажу.
Точно так же действует и виртуальный стереогониометр программы Adobe Audition.
Правда, для него предусмотрен и еще один режим работы: на виртуальные отклоняющие пластины вместо суммарного и разностного сигналов подаются сигналы левого и правого каналов, а графики, соответственно, строятся в системе координат L/R (Левый/Правый).
С точки зрения информативности такие способы отображения результатов измерения равноценны. Ведь между парой сигналов L и R, с одной стороны, и их суммой и разностью, с другой стороны, есть однозначная линейная связь. Изображения одного и того же процесса, полученные в двух системах координат, оказываются очень похожими друг на друга и отличаются, в основном, направлениями своих осей. Иными словами, пользователю предлагается выбрать более привычный вариант отображения результатов измерений.
Кроме того, возможен еще вариант Spin, который имитирует вращение развертки изображения на экране. Здесь получаются картинки восхитительной красоты, но использовать их для анализа трудно. В частности, они оказываются неразличимыми в тех случаях, когда при прочих одинаковых условиях меняются местами сигналы левого и правого каналов.
Для того чтобы помочь вам освоить виртуальный стереогониометр программы Adobe Audition, приведем вид фигур Лиссажу для нескольких характерных случаев.
На рис. 4.16 представлено изображение на рабочем поле окна Phase Analysis (система координат M/S (Моно/Стерео)) для ситуации, когда сигнал присутствует только в левом канале: L 

Рис. 4.16. Фигура Лиссажу: L 

Рис. 4.17. Фигура Лиссажу: L 

Рис. 4.18. Фигура Лиссажу: L 
Заметим, что перед использованием окна Phase Analysis важно установить правильное соотношение его сторон. Очень скоро вы узнаете, что оценка моносовместимости реального сигнала производится на основе сравнения средней высоты и средней ширины изображения наблюдаемой сложной фигуры. Поэтому рабочее координатное поле должно иметь форму квадрата.
Геометрические размеры окна, как обычно, изменяют, поочередно захватывая мышью нижнюю и левую его границы. Равенство сторон координатного поля можно установить "на глазок". Этого, в принципе, достаточно. Но если вы захотите откалибровать ваш виртуальный измерительный прибор с высокой точностью, то советуем действовать в следующем порядке.
С помощью опций окна Generate Tones, открываемого командой Generate > Tones, сгенерируйте стереофонический синусоидальный сигнал. О том, как выполняется подобная операция, рассказано в [10, разд. 7.4]. На рабочем поле главного окна выделите волновую форму одного из каналов (например, правого) и примените команду Effects > Silence (см. [10, разд. 6.3]). После этого сигнал правого канала заменится абсолютной тишиной. Так будет смоделирована ситуация L Ф 0, R = 0.Если вам трудно выполнить перечисленные операции, то просто загрузите в программу файл EX04_03.WAV, в котором мы записали необходимый сигнал. Откройте окно Phase Analysis. Вы увидите картину, которая должна почти в точности соответствовать рис. 4.16.
Изменяйте вертикальный и горизонтальный размеры окна в небольших пределах, наблюдая за изменениями фигуры Лиссажу (в данном случае — наклонной красной линии). Исчезновение малейших изломов на ней и послужит признаком "квадратности" координатного поля.
На рис. 4.19 в системе координат M/S представлена фигура Лиссажу для ситуации, когда сигналы присутствуют в обоих каналах, причем они равны: L = R (файл EX04_04.WAV).
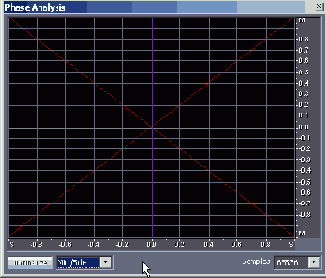
Рис. 4.19. Фигура Лиссажу: L = R, система координат M/S
На рис. 4.20 представлена фигура Лиссажу для ситуации, когда сигналы присутствуют в обоих каналах, но один из них инвертирован по отношению к другому, например, L = —R (файл EX04_05.WAV).

Рис. 4.20. Фигура Лиссажу: L = -R, система координат M/S
На рис. 4.21 представлена фигура Лиссажу для ситуации, когда сигналы присутствуют в обоих каналах, но наблюдается разбалансировка уровней, панорама смещена влево: L > R (файл EX04_06.WAV).

Рис. 4.21. Фигура Лиссажу: L > R, система координат M/S
На рис. 4.22 представлена фигура Лиссажу для ситуации, когда амплитуды сигналов равны (|L| = |R|), но имеется разбалансировка фаз, ф = 30° (файл EX04_07.WAV).

Рис. 4.22. Фигура Лиссажу:|L| = |R|, ф = 30°, система координат M/S
На рис. 4.23 представлена фигура Лиссажу для ситуации, когда амплитуды сигналов различны (|L|  EX04_08.WAV).
EX04_08.WAV).

Рис. 4.23. Фигура Лиссажу: |L| 
На рис. 4.24 представлена фигура Лиссажу для ситуации, когда амплитуды сигналов равны (|L| = |R|), но имеется разбалансировка фаз, ф = 90° (файл EX04_09.WAV).
Надеемся, что рассмотренные тестовые примеры помогли вам разобраться в сущности отображения сигналов в виде фигур Лиссажу. Конечно, при анализе реальных фонограмм картина на координатном поле окна Phase Analysis выглядит значительно сложнее. Ведь в ее формировании участвует не одна пара колебаний, а их теоретически бесконечное множество. Во всяком случае, спектр реального аудиосигнала чрезвычайно широк. И каждое колебание, имеющееся в спектре, характеризуется собственными параметрами: амплитудой, частотой и начальной фазой. Причем все три параметра непрерывно изменяются случайным образом.

Рис, 4.24. Фигура Лиссажу: |L| = |R|, Ф = 90°, система координат M/S
И все же опытные звукорежиссеры широко используют стереогониометр и его виртуальные аналоги для определения правильности передачи звуковой картины, распределения направлений на источники звука, наличия или отсутствия баланса, фазовых соотношений и моносовместимости фонограммы.
При широкой стереобазе фонограмма является моносовместимой, если все координатное поле окна Phase Analysis заполнено сложным многоцветным рисунком с приблизительно одинаковыми размерами по различным направлениям (рис. 4.25, файл EX04_10.WAV).

Рис. 4.25. Моносовместимая фонограмма с широкой стереобазой
У фонограммы, характеризующейся узкой стереобазой, признак моносовместимости заключается в том, что фигуры на координатном поле в основном вытянуты вдоль вертикальной оси (рис. 4.26, файл EX04_ll.WAV).

Рис. 4.26. Моносовместимая фонограмма с узкой стереобазой
Фонограмма мононесовместима, когда фигуры на координатном поле растянуты вдоль горизонтального направления (рис. 4.27, файл EX04_12.WAV).

Рис. 4.27. Мононесовместимая фонограмма
Если большая ось изображения на координатном поле отклонена от вертикали, то это является признаком нарушения стереобаланса: панорама сдвинута вправо (рис. 4.28, файл EX04_13.WAV) или влево (рис. 4.29, файл EX04_14.WAV).

Рис. 4.28. Панорама сдвинута вправо

Рис. 4.29. Панорама сдвинута влево
Проанализируйте свои работы с помощью окна Phase Analysis. Скорее всего, вы обнаружите много поучительного и увидите ошибки, о которых раньше и не подозревали.
Подводим итоги анализа и намечаем план работы
Итак, что же у нас вышло? Записано несколько дублей фонограммы с дикторским текстом, который будет использоваться для несинхронного сопровождения видеоряда. Выделены наиболее удачные дубли, т. е. те, в которых и диктор не оплошал, и посторонний шум мешает меньше всего, и перегрузка АЦП происходит редко, и уровень естественной реверберации относительно невысок.
Теперь нужно проделать следующее.
Из исходного файла вырезать лишние фрагменты, обработав образовавшиеся стыки так, чтобы они были малозаметны. При необходимости изменения длительности пауз вставить промежутки, содержащие абсолютную тишину (см. гл. 5). Провести амплитудную коррекцию сигнала: усилить, ослабить или нормализовать его (см. гл. 5). Уменьшить уровень шума (см. гл. 5). Устранить клиппирование (см.

